転がっている円上のある点が描く軌跡のことをサイクロイドと言います。高校数学でも扱うサイクロイド曲線、その中でもエピサイクロイドと呼ばれる曲線について紹介します。
円周上を転がる円
さて、早速ですが問題です。下図のようにコインを2つ上下にくっつけます。上のコインを下のコインに沿って回転させて移動させることを考えます。このとき、上のコインが下のコインの真下に来た時に、矢印はどこを向いているでしょうか。

直感的には、半分回るのだから矢印は下を向くと考えてしまいますが、実際には違います。この誤った直感は平面上での円の動きを曲面上の動きに無理やり当てはめてしまうために起こります。実はこれは、カリフォルニア大学バークレー校で、教育学を研究するアンドレア・ディセッサによって、物理的性質を推論することの難しさを調べるために使われた問題です。[1]
今回は、この問題を数学的に解いてみましょう。
媒介変数表示で軌跡を求める
矢印の向きを調べるために、矢印の先端がどのような軌跡を描くか、計算してみましょう。半径![]() の円が二つ上下に重なっていると仮定し、はじめ
の円が二つ上下に重なっていると仮定し、はじめ![]() にある点をPとします。反時計回りに上の円が回転するとします。反時計回りに
にある点をPとします。反時計回りに上の円が回転するとします。反時計回りに![]() 回転した時の状況を図に示します。
回転した時の状況を図に示します。
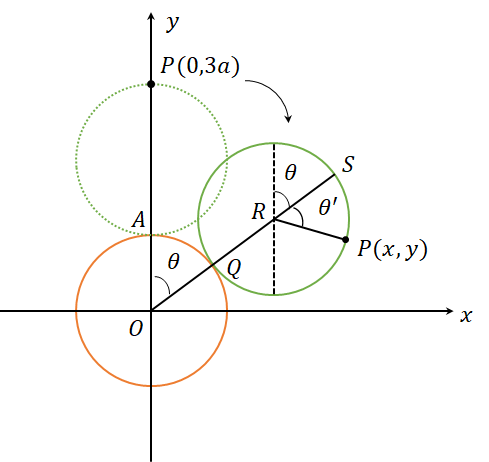
このときの点![]() の座標を回転角
の座標を回転角![]() を使って表します。
を使って表します。
まず、緑色の円が回転して移動した距離![]() は、点
は、点![]() が開店した距離
が開店した距離![]() と等しいことに注目します。
と等しいことに注目します。![]() とすると、
とすると、![]()
と表され、![]() から、
から、![]() とわかります。
とわかります。
次に、点![]() の座標をベクトルを使って求めます。まず、原点
の座標をベクトルを使って求めます。まず、原点![]() から回転している円の中心
から回転している円の中心![]() までのベクトルは、
までのベクトルは、
![]()
と表されます。続いて点![]() から点
から点![]() までのベクトルは
までのベクトルは
![]()
と表されます。したがって、点![]() は、
は、
![]()
となります。
これをグラフに描いたのが次の図です。(図は半径1の円で描いています。)ここで、最初の問題に戻ります。外周を沿って円が回転して反対側まで移動したときに矢印の先(下図の黒点)は、回転している円(図中緑色の円)の上側に来ていることがわかります。したがって、最初の問題の答えは”矢印は上を向く”でした。
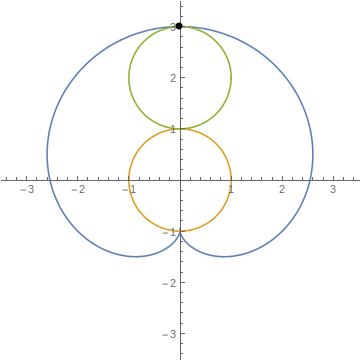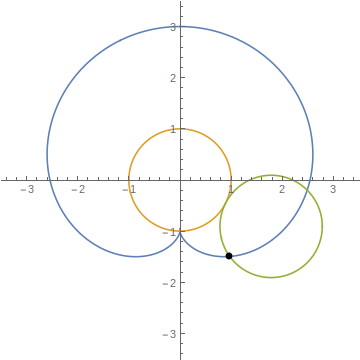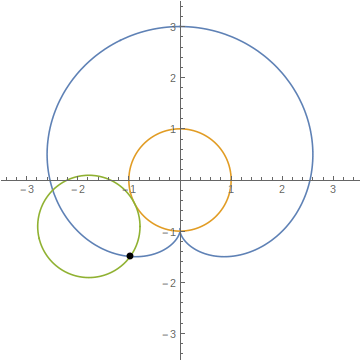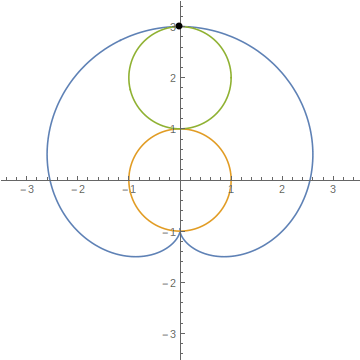
なぜ矢印が上を向くのか
数学を使って、矢印が上を向くことを示しました。しかし、直感とずれた回答で納得できない方もいるかもしれません。直感で矢印が下を向くと考えてしまう理由として、転がしているコインが自転だけでなく、公転していることを見落とすからだと思います。
上の図で、緑色の円に乗っている人から見ると、オレンジの円の下に来た時に黒い点は180度回転したように見えます。しかし、緑色の円はオレンジの円から、すなわち私たちの視点からみると、オレンジの円の周りを公転しています。この公転による回転の分が足されて矢印の頂点は、上図の青色のような軌跡を描きます。公転+自転で2倍の速さで矢印が回転しています。[2]
直感で答えをすぐに出すのではなく、一瞬立ち止まって考えてみると、公転している分の効果が含まれることに気づくことができるでしょう。
まとめ
円の外周を転がる円上の点が描く軌跡、エピサイクロイドについて紹介しました。その軌跡が人間の直感と異なることを数学的に証明することができました。数学の内容としては、高校数学のレベルであり、大学入試でも題材に使われることのある内容です。日常の些細なことについて、ちょっと考えてみるきっかけになれば、と思います。
付録:Mathematicaを使ってGIF画像を作る
今回、ブログ記事の中で示したエピサイクロイドのアニメーションはMathematica[3]を使って作成しました。Mathematicaに入力したコマンドを紹介します。(私の備忘録も兼ねてます。)
x[t_] := 2Sin[t]+Sin[2t];
y[t_] := 2Cos[t]+Cos[2t];
pp[u_] := ParametricPlot[{{x[t], y[t]},{Cos[t],Sin[t]},{2Sin[u]+Cos[t], 2Cos[u]+ Sin[t]}}, {t, 0, 2Pi}, Epilog -> {PointSize[Large],Point[{x[u], y[u]}]}, PlotRange -> {{-3.5, 3.5}, {-3.5, 3.5}}]
Anime=Animate[pp[u], {u, 0, 2Pi, Pi/20}]
1行目と2行目は、記事内で示した点![]() の座標です。tを変数として定義しています。
の座標です。tを変数として定義しています。
3行目はグラフの描画を定義しています。ここで使っているParametricPlotは媒介変数表示によるグラフの描画をするコマンドです。このParametericPlotの媒介変数はtで範囲は![]() ~
~ ![]() です。{t, 0, 2Pi}で定義しています。媒介変数表示で描くグラフは、①
です。{t, 0, 2Pi}で定義しています。媒介変数表示で描くグラフは、①![]() 、エピサイクロイド曲線、②
、エピサイクロイド曲線、②![]() 、中心の円、③
、中心の円、③![]() 、外側の円の3つです。ここで、3つ目のグラフにuという変数を使っています。これは3行目のグラフ描画では定数扱いで、回転角
、外側の円の3つです。ここで、3つ目のグラフにuという変数を使っています。これは3行目のグラフ描画では定数扱いで、回転角![]() に対応します。Epilogはある座標に点を打つコマンドです。角度uのときに頂点がエピサイクロイド曲線上のどこにあるかを示すためのコマンドです。PlotRangeはグラフの軸の範囲です。
に対応します。Epilogはある座標に点を打つコマンドです。角度uのときに頂点がエピサイクロイド曲線上のどこにあるかを示すためのコマンドです。PlotRangeはグラフの軸の範囲です。
4行目はアニメーションを作るコマンドです。これはuの値を![]() ~
~ ![]() まで
まで![]() 刻みで変化させ、それぞれの値でグラフを描画し、それをパラパラ漫画のようにつなげることでGIFアニメーションを作成します。こうして、作成したのが記事中のGIF画像です。
刻みで変化させ、それぞれの値でグラフを描画し、それをパラパラ漫画のようにつなげることでGIFアニメーションを作成します。こうして、作成したのが記事中のGIF画像です。
参考文献等
[1]知ってるつもり――無知の科学 スティーブン スローマン, フィリップ ファーンバック (著), 土方 奈美 (訳)
第四章にこの問題についての紹介があります。
[2]今回は二つの円の半径が同じだから、2倍になっています。二つの半径が異なれば、その比に応じた回転速度になります。内側の円の半径を![]() , 外側の半径を
, 外側の半径を![]() とすると、
とすると、
![]()
となります。
[3]Mathematicaは有名なソフトウェアで、数値計算やグラフの描画など数学や物理・化学などの様々な計算に用いられるソフトウェアです。非常に高度な計算を行うことができるのですが、個人で購入するには高価なソフトウェアです。ですが、ラズベリーパイというマイコンに標準で搭載されており、ラズベリーパイを購入すれば無料で使用することができます。ラズベリーパイは1万円もしないで購入可能なので、Mathematica目当てで買うだけでも非常にお得だと思います。

1 comment on エピサイクロイド、円周上を転がる円