皆さんこんにちは!
半導体物理の紹介をしていきます。前回、半導体として広く使われているシリコン(Si)と砒化ガリウム(GaAs)(ガリウム砒素と呼ぶことが多いです。)、それから最近ノーベル賞にもなった窒化ガリウム(GaN)の結晶構造を紹介しました。今回は結晶格子の面や方位を表すミラー指数について紹介します。
ミラー指数
ミラー指数は結晶格子の面や方位を表すために広く使われている表記法で、次のようなルールにしたがって表します。
| ミラー指数 | 表している面または方位 |
| { |
等価な面をすべて表します。例えば、立方晶系の場合、{100}は |
| 結晶内の方位を表し、 |
|
| 結晶内の等価な方向を表します。 | |
| 六方晶系の結晶格子(GaNなど)の面方位を表すのに使います。それぞれ、 |
これだけだと、よくわからないと思うので、具体的な例を示します。
左から(100)面、(110)面、(111)面になります。これらはよく使われる面で、Siを例に書きました。GaNのような六方晶だと次のような面が代表的な面として挙げられます。
これらは左からc面、a面、m面と呼ばれています。
六方晶系のミラー指数は![]() のように4つで表されます。それは六方晶系では次の図に示すような4つのベクトルを使って原子の位置を表現するからです。
のように4つで表されます。それは六方晶系では次の図に示すような4つのベクトルを使って原子の位置を表現するからです。
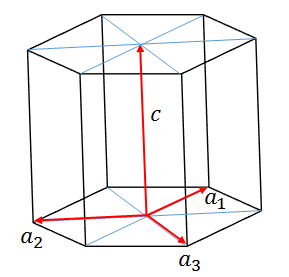
そして、ミラー指数には次のような関係式があります。
![]()
どうして、このような関係式が成り立つのか説明したいと思います。
皆さんご存知の通り、空間のある面を表すには3つのベクトルがあれば十分です。すなわち、![]() 軸の3つで十分です。ですが、上図のように4つの軸を使って表すと便利なことがあるので、まだ使われています。さて、
軸の3つで十分です。ですが、上図のように4つの軸を使って表すと便利なことがあるので、まだ使われています。さて、![]() 面を考えます。この面と
面を考えます。この面と![]() 面の交わる部分は下図の赤線
面の交わる部分は下図の赤線![]() となります。
となります。
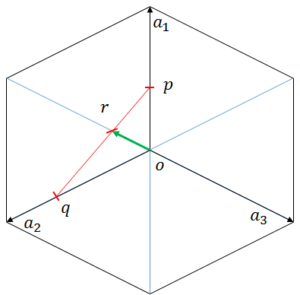
点![]() はそれぞれ
はそれぞれ![]() を
を![]() する点です。
する点です。
![]() 面上、すなわち赤線
面上、すなわち赤線![]() には
には![]() ,
, ![]() ,
, ![]() の先が存在する。すなわち、
の先が存在する。すなわち、![]() となる。直線
となる。直線![]() は
は![]() の二等分線であることから、
の二等分線であることから、
![]()
![]()
![]() [math]+\bf{a_{2}})[/math]
[math]+\bf{a_{2}})[/math]
![]() [math] = -1/l \cdot (\bf{a_{1}}[/math]
[math] = -1/l \cdot (\bf{a_{1}}[/math]![]()
となり、![]() が成り立ちます。
が成り立ちます。
4つの軸を使って表すと便利なこととして、六方晶の等価な面を考えやすいということがあります。例えば、(11-20)面と等価な面の一つに(1-210)面があり、これはわかりやすいと思います。ところが、もし3つの軸で表していたとすると、(110)面と(1-20)面が六方晶では等価な面と表現することになるのですが、先ほどとは違ってわかりづらいですよね。そういう理由もあっていまだに六方晶系では4つの軸を使ったミラー指数の表記をしています。
まとめ
今回は結晶格子の面や方位を表すのに使われるミラー指数を紹介しました。次は逆格子について紹介したいと思います。
最後まで読んでいただきありがとうございました。これで、”半導体物理:結晶構造(3)”を終わります。また次回の記事でお会いしましょう!

最近のコメント