XRDや電子線回折などを用いて結晶を評価するときや、第一原理計算で材料物性を計算するときなど、結晶の格子の面間隔や体積を計算したいときがあります。
そんな時に一目見て役に立つように式をまとめました。
立方晶(Cubic crystal)
- 面間隔の式:
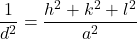
- 体積の式:
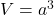
正方晶(Tetragonal crystal)
- 面間隔の式:
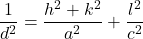
- 体積の式:
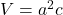
直方晶 (Orthorhombic crystal)
- 面間隔の式:
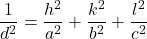
- 体積の式:
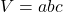
以前は、斜方晶と呼ばれていましたが、最近は直方晶と呼ばれています。[1]
六方晶 (Hexagonal crystal)
- 面間隔の式:
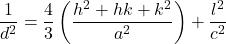
- 体積の式:
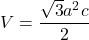
単斜晶 (Monoclinic crystal)
- 面間隔の式:
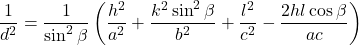
- 体積の式:
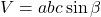
三斜晶 (Triclinic crystal)
- 面間隔の式:
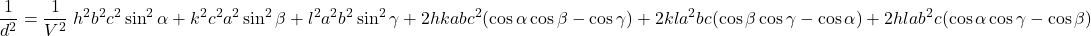
- 体積の式:
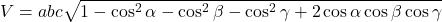
これらの式を用いることで、さまざまな結晶構造に対して面間隔や体積を求めることができます。面間隔や体積を計算したいときにご活用ください。
また、格子面がなす角度を計算する方法について下記のページにまとめています。
参考文献
[1] “『斜方晶系』をやめて『直方晶系』を使おう “, 大橋 裕二, 日本結晶学会誌 57, 131-133(2015).

最近のコメント