物理の基本的な問題の一つに、放物運動があります。今回、Pythonを使った数値計算の練習として、この放物運動を題材にしようと思います。
計算するのは、放物運動で物体を最も遠くに飛ばすことのできる発射角度です。よく45度で発射すると最もよく飛ぶと言われますが、どうでしょうか。計算して確かめてみましょう。
運動方程式を解く
数値計算を始める前にまず初めに運動方程式を解いて、物体の飛距離を計算します。
高さ![]() から初速度
から初速度![]() , 角度
, 角度![]() で質量
で質量![]() の物体を射出することを考えます。
の物体を射出することを考えます。
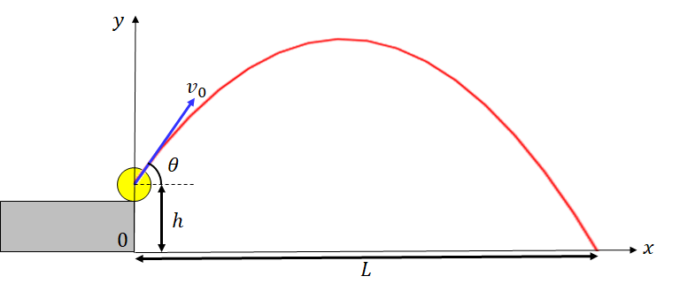
座標を下図のように設定すると、時刻![]() のときの物体の座標は、次式のようにあらわされます。
のときの物体の座標は、次式のようにあらわされます。
![]() (1)
(1)
![]() (2)
(2)
![]() は重力加速度です。物体の飛距離
は重力加速度です。物体の飛距離![]() は、
は、![]() のときの時刻における
のときの時刻における![]() である。式(2)から
である。式(2)から
![]() ⇒
⇒ ![]()
この時刻を式(1)に代入して、整理すると
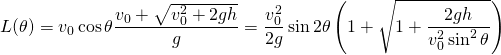 (3)
(3)
この式をもとに飛距離を最大にできる角度を求めていきます。
検討①:高さが0のとき
飛距離を最大にできる角度を厳密に求める前に、ある程度の角度を予想しましょう。まず、高さが0の場合を考えます。このとき、式(3)は、
![]() (4)
(4)
となります。式(4)が最大になるのは![]() になるとき、すなわち45度のときです。
になるとき、すなわち45度のときです。
世間で広く言われている45度で投げると一番遠くまで飛ぶというのはこの計算がもとになっています。物体を高い位置から投げることを想定しない場合であれば、確かに45度で投げるのが正しいです。
検討②:高さが十分に高いとき
次に高さが十分に高いときを考えてみます。高さが十分に高いときというのは、![]() のときです。このとき、式(3)は、
のときです。このとき、式(3)は、
![]() (5)
(5)
となる。式(5)から高さが十分に高いときには飛距離は![]() で変化し、飛距離が最大になるのは水平に射出した時になります。
で変化し、飛距離が最大になるのは水平に射出した時になります。
最大飛距離になる角度を計算
近似を使わずに最大飛距離になる角度を計算するには、式(3)を![]() で微分し、導関数が0になるときの
で微分し、導関数が0になるときの![]() を計算することで、求められます。ですが、
を計算することで、求められます。ですが、![]() で微分するのは計算が煩雑になります。今、射出角度は0 ~ 90度を想定しています。このとき、
で微分するのは計算が煩雑になります。今、射出角度は0 ~ 90度を想定しています。このとき、![]() は単調に増加することから、
は単調に増加することから、![]() のとき、
のとき、![]() が成り立ちます。そこで、
が成り立ちます。そこで、![]() として、式(3)を整理すると、
として、式(3)を整理すると、
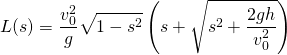 (6)
(6)
となります。式(6)を![]() で微分し、
で微分し、![]() をもちいて整理すると、
をもちいて整理すると、
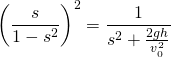
これは、二次式なので解くことができ、
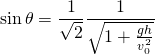
を満たす![]() のとき、飛距離が最大になるということが計算できました。ここまでくれば、
のとき、飛距離が最大になるということが計算できました。ここまでくれば、![]() を使って計算することができます。
を使って計算することができます。
数値計算で求めてみる
今回は、運動方程式を解くことで解析的に飛距離が最大になる角度を求めることができました。ですが、必ず解析的に解くことができるとは限りません。今回は考慮していませんが、実際には空気抵抗や摩擦の影響も含めないと、現実の物体の動きを予測することはできません。そうなると、解析的に解ける場合はほとんどありません。解析的に解けない場合は、数値的に解を求めることになります。放物運動を題材にpythonで数値的に最大飛距離になる角度を求めてみたいと思います。
pythonの科学計算ライブラリのScipyを使って、計算します。Scipyには、最小値を求める関数optimize.brentが用意されています。
このoptimize.brentを使って次のようなプログラムを書きます。
from scipy import optimize import numpy as np import matplotlib.pyplot as plt def L(theta): v0 = 30.0 #m/sec h = 10.0 #m g = 9.8 #m/s^2 x = v0**2*np.cos(theta)*(np.sin(theta)+np.sqrt(np.sin(theta)**2+2.0*g*h/v0**2))/g x2 = -1.0*x #最小値を求める関数を使うので、-1倍して最大値が最小値になるようにしている return x2 t = np.linspace(0.0, np.pi/2, 100) plt.figure() plt.plot(t, -1.0*L(t), 'r-') #グラフのプロット 飛距離vs射出角度 theta0 = optimize.brent(L) theta0_deg = 180.0*theta0/np.pi print(theta0) print(theta0_deg) print(-1.0*L(theta0))
初速度と物体を発射する高さは適当な値を入れてあります。このプログラムで計算した結果では、最大飛距離は101.3 m, そのときの角度は42.2度と計算されました。45度よりもわずかに低い角度で投げるのが一番良いという結果が得られました。
ちなみに、先ほどのプログラムで高さを0 mにすると、45度という結果がちゃんと返ってきます。このように数値計算で解くと、簡単に解を求めることができます。
まとめ
物理の基本的な問題である放物運動について、運動方程式を解いて最大の飛距離がでる発射角度を解析的・数値的に求めました。数値的に解く方法は解析的に解くことのできない問題を解くためには必要な技術です。これを土台に数値計算について深く理解していきたいと考えています。
最後までお読みいただきありがとうございます。それでは、次回の記事でお会いしましょう。

最近のコメント