光電効果は光が粒子としての性質をもつとすることで説明することができます。では、逆に電子も波動としての性質をもつと考えることもできます。ここでは粒子の波動性について電子を題材に考えてみましょう。
粒子と波動の対応
光を粒子としても波動としても扱ってよいことが、光電効果の例で分かりました。では、この粒子と波動の対応関係から考えると、次のようなことが言えます。
ある位置と時刻![]() における粒子数密度が同じ位置と時刻
における粒子数密度が同じ位置と時刻![]() における波動の強度に対応しています。
における波動の強度に対応しています。
そのため、波動の振幅を表す波動関数![]() は、振幅の二乗が粒子を見出す確率を与えるという意味で、確率波と呼ばれます。
は、振幅の二乗が粒子を見出す確率を与えるという意味で、確率波と呼ばれます。
波動の干渉
2つの波、![]() を合成して、波動関数
を合成して、波動関数![]() が与えられるとすると、
が与えられるとすると、
![]()
と表されます。このように二つの波で足しあわされるのは波の強度ではなく、振幅であるために干渉が起きます。粒子の運動量は![]() と波数ベクトル
と波数ベクトル![]() を用いて表されることから、
を用いて表されることから、
![]()
と表されます。
電子の波動性~アハラノフ-ボーム効果~
電子の波動性を示す現象として、アハラノフ-ボーム効果があります。これはリング状の導体に時間変化しない磁場をかけたときに、リングの二つの経路を通る電子の間に干渉が起こる現象です。
詳しくこの現象を考えていきましょう。まず、ベクトルポテンシャル![]() を導入し、磁場
を導入し、磁場![]() と表します。リングに電子が入るときにリングの中心から入り、時計回りと反時計回りの経路を通って反対の中心から出ていくこととします。時計回りの場合、角度
と表します。リングに電子が入るときにリングの中心から入り、時計回りと反時計回りの経路を通って反対の中心から出ていくこととします。時計回りの場合、角度![]() が
が![]() から0, 反時計回りの場合、角度
から0, 反時計回りの場合、角度![]() が
が![]() から0に変化するとします。
から0に変化するとします。
ベクトルポテンシャルによって波数ベクトル![]() は次のように変化します。
は次のように変化します。
![]()
ここで、![]() は磁場がない時の波数ベクトルです。
は磁場がない時の波数ベクトルです。
したがって、時計回りで通過した電子と、反時計回りで通過した電子の位相差は、波数ベクトルを線積分したもの同士の差に等しいので、
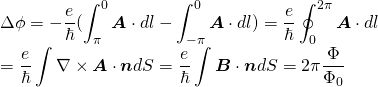
と計算されます。ここで、![]() はリングを貫く磁束で、
はリングを貫く磁束で、![]() は磁束量子です。
は磁束量子です。
このように、位相差は0でなく、静止した磁場によって電子の干渉が生じることを表しています。ただし、実際にこの干渉が観察されるには電子のコヒーレンス長(非弾性散乱長)よりも、リングのサイズが小さいことが必要になります。
まとめ
光が波動性と粒子性をもつように、電子も粒子性と波動性をもつと考えることができます。磁場が電子の波動性に与える影響について考えてみました。アハラノフ-ボーム効果は電子を粒子として考えていては説明ができない現象であり、電子の波動性を示す一つの事例になります。

1 comment on 【量子力学】電子の波動性