MIS構造において、一般的には絶縁膜は1種類の単層膜だが、2つの異なる絶縁膜を積層した構造をとる場合もある。そのときのフラットバンドシフトの計算と電圧をかけた時に絶縁膜の間に蓄積する分極電荷を計算する。
フラットバンドシフトの計算
まず、一般的なMISキャパシタ(絶縁膜は1種類)について考える。MISキャパシタにおけるフラットバンド状態は、半導体表面のポテンシャルがゼロの状態である。フラットバンド状態になるには、金属と半導体の仕事関数差![]() と絶縁膜の電荷がつりあう必要がある。フラットバンド状態の容量は次式であらわされる。
と絶縁膜の電荷がつりあう必要がある。フラットバンド状態の容量は次式であらわされる。
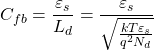
![]() は半導体の誘電率、
は半導体の誘電率、![]() はデバイ長、
はデバイ長、![]() は半導体のドープ濃度、
は半導体のドープ濃度、![]() はボルツマン定数、
はボルツマン定数、![]() は温度、
は温度、![]() は電子の電荷である。ここで、デバイ長とは表面のバンド曲がりによって生じる空間電荷の存在する領域の長さを表す。フラットバンド状態の時の電圧をフラットバンド電圧と呼び、
は電子の電荷である。ここで、デバイ長とは表面のバンド曲がりによって生じる空間電荷の存在する領域の長さを表す。フラットバンド状態の時の電圧をフラットバンド電圧と呼び、
![]()
であらわされる。![]() をフラットバンドシフトとよび、その大きさは絶縁膜中の電荷で決まる。絶縁膜中の電荷によるフラットバンドシフトはガウスの法則から、
をフラットバンドシフトとよび、その大きさは絶縁膜中の電荷で決まる。絶縁膜中の電荷によるフラットバンドシフトはガウスの法則から、
![]()
で計算することができる[3]。![]() は絶縁膜容量、
は絶縁膜容量、![]() は単位体積当たりの電荷量、
は単位体積当たりの電荷量、![]() は絶縁膜の電気長で
は絶縁膜の電気長で![]() であらわされ、
であらわされ、![]() は絶縁膜の膜厚、
は絶縁膜の膜厚、![]() は絶縁膜の比誘電率である。絶縁膜の容量はCV特性におけるキャパシタンスの最大値であり、測定しているキャパシターの面積と誘電率が分かれば、絶縁膜の膜厚を計算することができる。また、
は絶縁膜の比誘電率である。絶縁膜の容量はCV特性におけるキャパシタンスの最大値であり、測定しているキャパシターの面積と誘電率が分かれば、絶縁膜の膜厚を計算することができる。また、![]() は金属-絶縁膜界面から絶縁膜-半導体界面に向かう方向である。
は金属-絶縁膜界面から絶縁膜-半導体界面に向かう方向である。
絶縁膜が単層の場合、絶縁膜と半導体の界面にのみ電荷が存在するとすると、![]() となる。
となる。![]() はディラックのデルタ関数である。これを式(1)に代入すると、
はディラックのデルタ関数である。これを式(1)に代入すると、
![]()
となる。
次に、2層の絶縁膜の場合を考える。金属/絶縁膜1/絶縁膜2/半導体のようになっているとすると、フラットバンドシフトは次のようになる[4]。
![]()
式(2)を3つの場合について解いてみる。絶縁膜中の電荷![]() が、①絶縁膜1と絶縁膜2の界面にある場合、
が、①絶縁膜1と絶縁膜2の界面にある場合、![]() 、②絶縁膜2と半導体の界面にある場合、
、②絶縁膜2と半導体の界面にある場合、![]() 、③絶縁膜1と絶縁膜2に均一に分布している場合、
、③絶縁膜1と絶縁膜2に均一に分布している場合、![]() を解くとそれぞれ次のようになる。
を解くとそれぞれ次のようになる。
①![]()
②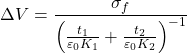
③![]()
実際には3つの状態のうちのどれかを断定することは難しく、絶縁膜単層の場合と比較しながら決めていくことになる。
絶縁膜界面に蓄積する界面分極電荷
2層の絶縁膜の場合、電圧をかけると2つの絶縁膜間で電流の流れやすさが異なるため、界面に電荷が蓄積される。各絶縁膜にかかる電界を![]() とすれば、絶縁膜中を流れる電流は、
とすれば、絶縁膜中を流れる電流は、![]() となるので、
となるので、![]() となる。
となる。![]() は電気伝導率。各絶縁膜に加わる電圧は電界と厚みの積なので、
は電気伝導率。各絶縁膜に加わる電圧は電界と厚みの積なので、
![]()
とあらわされる。ガウスの定理![]() を適用すると、界面に蓄積する電荷は
を適用すると、界面に蓄積する電荷は![]() と
と![]() の差なので、
の差なので、
![]()
この場合の分極は界面電荷![]() が絶縁膜1の厚み分だけ変化したと考えて、
が絶縁膜1の厚み分だけ変化したと考えて、
![]()
となる。
参考文献
[1] Bonilla, R. S., Reichel, C., Hermle, M., & Wilshaw, P. R. (2015). Erratum: “On the location and stability of charge in SiO 2 /SiN x dielectric double layers used for silicon surface passivation” J. Appl. Phys. 115 , 144105 (2014). https://doi.org/10.1063/1.4915629
[2] https://sciencompass.com/phys-engineer/semiconductor_physics/gan_debye-length_doping
[3] S. M. Sze, “Physics of Semiconductor Devices” 2nd ed. Ch.4.
[4]Abbott, R. A., & Kamins, T. I. (1970). Sodium migration through electron-gun evaporated Al2O3 and double layer Al2O3SiO2 structures. Solid-State Electronics, 13(5), 565–576. https://doi.org/10.1016/0038-1101(70)90137-1

最近のコメント