フェルミ準位の算出や半導体中のキャリア密度の算出は半導体物理の基礎とされています。例えば、半導体の伝導帯中に存在する電子数は、
![]()
であらわされます。![]() は伝導帯の状態密度関数、
は伝導帯の状態密度関数、![]() は電子の状態の占有確率でフェルミ-ディラック分布の式、
は電子の状態の占有確率でフェルミ-ディラック分布の式、
![]()
で表されます。これは電子がフェルミ-ディラック分布に従うということが熱・統計力学から示されているからで、そちらについては統計力学の教科書を参考にしてください。
さて、状態密度関数![]() は、
は、
![]()
と表されます。ここで、![]() は等価な伝導帯の下端の数、
は等価な伝導帯の下端の数、![]() は状態密度の等価な電子の有効質量で、
は状態密度の等価な電子の有効質量で、![]() で表されます。
で表されます。
この状態密度関数![]() はどのように導出されているのでしょうか。ここでは状態密度関数を導出してみたいと思います。
はどのように導出されているのでしょうか。ここでは状態密度関数を導出してみたいと思います。
無限の高さの障壁をもつ矩形井戸ポテンシャルを考える
伝導帯の電子の状態密度は無限の高さの障壁をもつ矩形井戸ポテンシャル内に存在する電子の状態密度と考えられます。
1電子近似で、無限に高い障壁をもった矩形井戸ポテンシャル内の電子に対する、時間に依存しないシュレーディンガー方程式は、
![]()
と表される。1辺![]() の立方体の半導体結晶とすると、ポテンシャル
の立方体の半導体結晶とすると、ポテンシャル![]() は、
は、
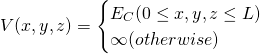
したがって、![]() とすると、
とすると、
![]()
となる。このとき、波動関数![]() は、
は、
![]()
と解けます。これを先ほどのシュレーディンガー方程式に代入すると、
![]()
となります。今、無限の高さの障壁をもつ矩形井戸を考えているため、![]() で
で![]() となることから、
となることから、
![]()
という制限が生じます。ここで、![]() となります。
となります。
三次元波数ベクトル空間で許容される状態の値は、![]() =一定の、等エネルギー面を表します。状態密度は、等エネルギー球内の状態数
=一定の、等エネルギー面を表します。状態密度は、等エネルギー球内の状態数![]() をエネルギーで微分することによって得られる。すなわち、
をエネルギーで微分することによって得られる。すなわち、![]() で表されます。
で表されます。
ここで、先ほどの境界条件から波数ベクトルの値は、波数ベクトル空間で各成分が正の値をとる8分の1の領域に限定されます。また、一つの![]() 点に対応する体積
点に対応する体積![]() で表されます。
で表されます。
エネルギー面![]() と
と![]() を境界とする薄い球殻の体積を考え、これを一つの
を境界とする薄い球殻の体積を考え、これを一つの![]() 点に対応する体積で割ると、
点に対応する体積で割ると、
![]()
となります。![]() なので、
なので、
![]()
となります。ここまでの計算では電子のスピンについて考慮されていません。電子のスピンを考慮すると状態数はこの2倍になります。また、半導体の等価な伝導帯下端の数を考慮すると、
![]()
が得られます。以上により、半導体の状態密度が導かれました。

最近のコメント