半導体デバイスでは、電流を流すために金属電極を半導体表面に形成しています。半導体と金属を接触させると、ショットキー接触とオーミック接触という2種類のパターンに分かれます。金属の種類や半導体の種類、構造によってショットキー接触とオーミック接触を作り分けることが出来ます。ここでは、オーミック接触について説明します。
オーミック接触とは
オーミック接触はどのような金属-半導体接触のことをいうのでしょうか。
オーミック接触は、デバイス特性に影響を与えない、言い換えると電極と半導体の界面での電圧降下がデバイスのアクセス領域での電圧降下と比べて無視できるほど小さい、とされています。
半導体デバイスに導通するために最低でも2つの金属電極が必要であり、オーミック接触はすべての半導体デバイスに必要な技術になります。
オーミック接触を数式で表現
オーミック接触を評価する指標として、固有接触抵抗率があります。固有接触抵抗率は、電流密度を電圧で微分した逆数で、電圧Vが0のときの値で定義されます。
![]()
この方程式をコンピュータを使って数値的に解いてもいいのですが、金属-半導体界面を流れる電流の式を使って解析的な解をえることが出来ます。熱電子放出(TE:Thermionic Emission)、電界放出(FE:Field Emission)、その中間の熱電界放出(TFE:Thermionic Field Emission)モデルを考えます。それぞれのモードで固有接触抵抗率は次のようにあらわされます。[1]
| TE | ||
| TFE | ||
| FE |
以上の式から固有接触抵抗率は、障壁高さの関数であり(すべてのモード)、ドーピング濃度の関数であり(TFEとFE)、温度の関数である(特にTEとTFE)ことがわかります。定性的には、TEモードでは固有接触抵抗率はドーピング濃度によらず一定で障壁高さが高くなると値が増加します(障壁高さが低ければ、抵抗率は減少する)。一方、FEモードでは、障壁高さに加えてドーピング濃度![]() に対して、
に対して、![]() で抵抗率が減少します。
で抵抗率が減少します。
実デバイスでの接触抵抗
実際のデバイスでオーミック接触を形成したときの抵抗を考えてみましょう。
いま、電極の面積が![]() であるとしたとき、接触抵抗
であるとしたとき、接触抵抗![]() をもちいてオーミック抵抗
をもちいてオーミック抵抗![]() は、
は、
![]()
で表されます。しかし、この式は材料の中を均一に電流が流れる場合にのみ有効な式であります。
単純化したモデルであるため、より実際のデバイスに近いモデルを2つ考えます。
縦型デバイスの場合
まず、図1のように縦型のデバイスを考えます。デバイス表面側の電極は直径![]() の円形とし、下側全面に電極を形成している場合を考えます。
の円形とし、下側全面に電極を形成している場合を考えます。
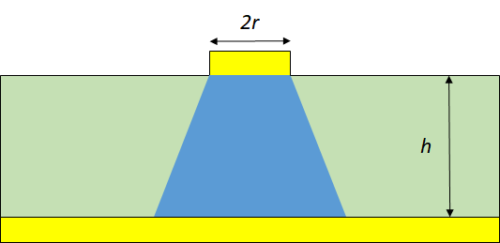
図1 縦方向に電流が流れるときの模式図。図中の青い領域に電流が流れる。
このとき、半導体中を流れる電流の抵抗値は広がり抵抗![]() と呼ばれ、
と呼ばれ、
![]()
で表されます[1]-[3]。ここで、![]() は半導体の抵抗率を表します。
は半導体の抵抗率を表します。
横型デバイスの場合
2つ目の例として、図2のように横方向に電流が流れる場合を考えます。
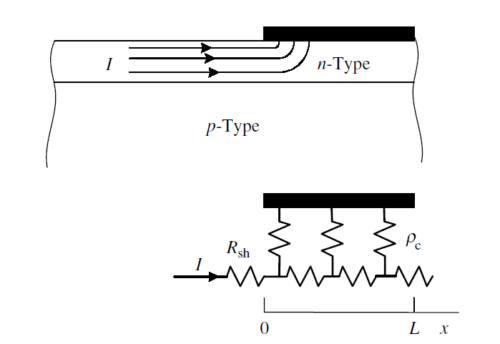
図2 横方向に電流が流れる模式図(上)と、電極下を伝送線路で表現した図(下) [4]
いま![]() 方向のみを考えることにします。オーミック電極の電極端を
方向のみを考えることにします。オーミック電極の電極端を![]() とし、電極の下の抵抗、すなわちコンタクト抵抗を計算してみます。
とし、電極の下の抵抗、すなわちコンタクト抵抗を計算してみます。
図のように電極の下部分をシート抵抗![]() とコンタクト抵抗
とコンタクト抵抗![]() に分解して考えます。これは伝送線路の考え方になります。電極の外側(
に分解して考えます。これは伝送線路の考え方になります。電極の外側(![]() )では電流が0、すなわちOpenになっているので、伝送線路の方程式を解くと電流、電圧はそれぞれ、
)では電流が0、すなわちOpenになっているので、伝送線路の方程式を解くと電流、電圧はそれぞれ、
![]()
![]()
ここで、![]() は、
は、
![]()
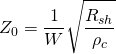
と表され、![]() は奥行き方向の電極幅です[5]。
は奥行き方向の電極幅です[5]。
コンタクト抵抗は、![]() での抵抗値なので、
での抵抗値なので、
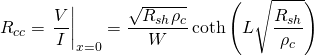
と求めることが出来ます。
まとめ
金属-半導体界面を流れる電流を計算したモデルからオーミック抵抗を数式で表現しました。また、実際のデバイスで接触抵抗がどのように表現されるか、縦型と横型の二通りを紹介しました。ぜひ、デバイスを評価するさいに役立ててください。
参考文献
[1] S.M. Sze and Kwok K. Ng, “Physics of Semiconductor Devices” 3rd Edition, Chapter 3.
[2] Ragnar Holm, “Electric Contacts” 4th Edition.
[3] R.H. Cox and H. Strack, Solid State Electron. 10, 1213-1218 (1967).
[4] Dieter K. Schroder, “SEMICONDUCTOR MATERIAL AND DEVICE CHARACTERIZATION” 3rd Edition.
[5] I. F. Chang, Solid State Science vol. 117, No. 3, 368 (1970).

最近のコメント