短チャネル効果とは何か
半導体デバイスは性能向上や1枚のウェハからとれるチップの数を増やしてコストを下げるため、ムーアの法則に従ってどんどん微細化が進んでいる。
ところが、デバイスの微細化に伴う副作用が発生する。それが短チャネル効果と呼ばれる現象である。短チャネル効果はいくつかあり、
・ドレイン誘起障壁低下 Drain-Induced Barrier Lowering (DIBL)
・表面散乱 Surface scattering
・電子速度飽和 Velocity saturation
・衝突電離 Impact ionization
・ホットキャリア注入 Hot Carrier Injection(HCI)
があげられる。
ドレイン誘起障壁低下 Drain-Induced Barrier Lowering (DIBL)
ドレイン誘起障壁低下(DIBL)は、大きなドレイン電圧を印可したときに、電子がソースからドレインへと向かうときの障壁高さが下がる現象である。
ソースドレインの電圧が0Vのとき、ゲート下の障壁高さはゲート電圧を変えることによって制御できる。理想的には障壁高さはゲート電圧だけで制御されるべきである。しかし、ゲート長が短く、かつドレイン電圧が大きくなると、空乏層がゲート下まで広がり障壁高さが下がる。このことから、この現象はドレイン誘起障壁低下と呼ばれている。
障壁高さの減少と閾値電圧の減少は、電荷中性に関するYauのチャージシェアリングモデルで説明される[2, 3]。
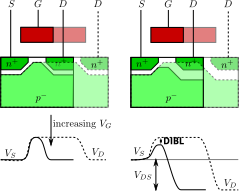
図1 左:![]() V, 右:
V, 右:![]() 印可したとき。実線と点線が障壁高さを表し、実線が短ゲート、点線が長ゲートのとき。ドレイン電圧を印可したときにゲート下の空乏層幅が広がり、障壁高さが下がる。[1]
印可したとき。実線と点線が障壁高さを表し、実線が短ゲート、点線が長ゲートのとき。ドレイン電圧を印可したときにゲート下の空乏層幅が広がり、障壁高さが下がる。[1]
ドレインから空乏層の広がりが顕著だと、ソース・ドレイン間にゲートよりも深い領域でリーク電流パスができてしまうパンチスルーが起こる。そうすると、サブスレッショルド領域の電流の立ち上がりが緩やかになる。すなわち、サブスレッショルド係数が劣化し、ゲートによる制御が弱くなる[4]。
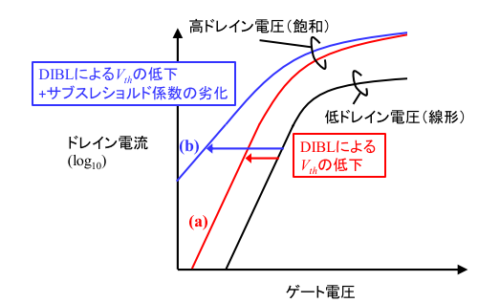
図2 短チャネルMOSFETのId-Vg特性
DIBLはドレイン電圧と閾値電圧を使って次のように表現される。
![]()
![]() は非常に低いドレイン電圧で、一般的に0.05V,もしくは0.1Vである。
は非常に低いドレイン電圧で、一般的に0.05V,もしくは0.1Vである。![]() は供給電圧(高ドレイン電圧)である。
は供給電圧(高ドレイン電圧)である。
また、DIBLはゲート制御の効果が弱まるので、デバイスの動作周波数が下がる。
![]()
表面散乱 Surface Scattering
電子の速度はチャネルの移動度によって決まります。MOSFETの場合、チャネルを走行する電子はゲートからの電解に影響を受けて、ゲート絶縁膜と衝突しながらジグザグに走行する。その結果、実効的な移動度が減少してしまい、IV特性の劣化につながる。
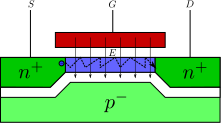
図3 表面散乱の模式図[1]
なぜ、表面散乱が短チャネル効果に含まれているのか?それは、ソース-ドレイン間が近づくとVdsが大きくなり、それを補償するためにゲート電圧も大きくする必要が出てくる。その結果、より多くの電子が絶縁膜と衝突することになるため、短チャネル効果に含まれている。
速度飽和 Velocity Saturation
電子や正孔などの電荷キャリアの速度は、それを駆動する電界に比例するが、それは小さな電界でのみ有効である。電界が強くなると、キャリアの速度は飽和する傾向にある。つまり、臨界電界を超えると、速度が飽和してしまい、結局は速く動けなくなる。チャネル長が短いと電界も強くなるため、速度飽和が顕著になる。
電子の飽和速度
臨界電界は次のようにあらわされる。
![]()
![]() はキャリアの移動度、
はキャリアの移動度、![]() は電界、
は電界、![]() は速度飽和が起こる臨界電界である。
は速度飽和が起こる臨界電界である。
電界が![]() のときは、
のときは、![]() となる。
となる。
速度飽和が起こった時のドレイン電流
速度飽和が起こると、ドレイン電流はどうなるのだろうか。
電流はトランジスタのチャネルを移動する電荷量で記述することができる。
電荷量の変化は、
![]()
である。続いて電流は、
![]()
で記述できる。チャネルの内部で電子速度![]() が一定であると仮定する。チャネル長が長い時の電子速度を
が一定であると仮定する。チャネル長が長い時の電子速度を![]() とすると、
とすると、
![]()
チャネル長が長い時には、![]() のときに電流が飽和するが、チャネル長が短い時にはその前に飽和する。
のときに電流が飽和するが、チャネル長が短い時にはその前に飽和する。
飽和するドレイン電圧, ![]() は、
は、![]() をとくとことで求めることができる。
をとくとことで求めることができる。
![]() であるので、
であるので、
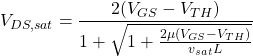
![]() が正なので、
が正なので、![]() は
は![]() より小さくなる。
より小さくなる。
衝突電離 Impact Ionization
前述したように、短チャネルのトランジスタは、ソースとドレインの距離が非常に小さいため、横方向に強い電界が発生する。この電界により、電荷キャリアの速度が速くなり、エネルギーも高くなる。
高いエネルギーをもつキャリアは「ホットキャリア」と呼ばれ、問題を起こす可能性がある。ホットキャリアは通常、ドレインの近くに現れ、最も高いエネルギーを持つ。
キャリアは走行中に構造体の原子に衝突する可能性があります。キャリアに十分なエネルギーがあれば、衝突によって原子に渡されるエネルギーによって、電子が価電子帯から伝導帯へと叩き出される。これにより、電子と正孔のペアが発生する。これが衝突電離である。
発生したペアのうち、正孔はバルクに引き寄せられ、発生した電子はドレインに移動する。
すなわち、基板電流を測定することで、インパクトイオン化効果を測定することができる。
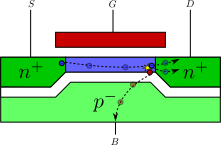
図4 衝突電離によって電子正孔対が発生し、バルクへホールが流れる[1]
ホットキャリア注入 Hot Carrier Injection
高電界によって生じるホットキャリアは、衝突電離を起こす以外にも別の可能性がある。ホットキャリアがもつエネルギーは、酸化物に入り込むのに十分なもので、酸化物にトラップされる可能性がある。閉じ込められた電子は、しきい値電圧の上昇という形で、ゲート電圧に対するトランジスタの特性を変化させる。時間が経つと、酸化物に電子が蓄積され、いわゆるトランジスタの「老化」が起こる。
興味深いことに、FLASHメモリーでは、同じ効果を利用してビットを記憶している。「ホットキャリア」の注入によってフローティングゲートに蓄えられた負の電荷がしきい値電圧を変化させ、この変化が1または0として解釈されるのだ。
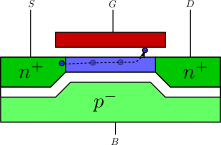
図5 ホットキャリアが酸化物に飛び込む様子[1]
まとめると、ホットキャリアによって
・衝突電離による電子/正孔対の発生
・酸化物への電子トラップ
が生じ、
・ドレイン抵抗の増加
・閾値電圧上昇
が起こる。
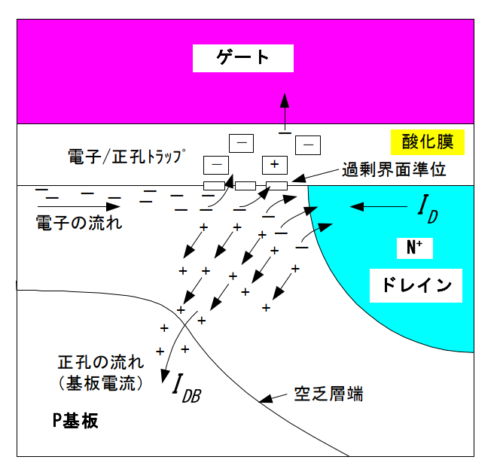
図6 ホットキャリアのまとめ[5]
これらの対策として、低ドープのn層をn+層の隣に設けることで、横方向の電解を弱くする方法が提案されている。(LDD: Lightly Doped Drain)
電界を弱くするのはドレインだけでよいが、ドレイン端子は動作点でしか規定されないため、MOSFETの両端子に注入する。その理由は、軽くドープされたインプラントの方が空乏領域が広くなるからだ。空乏領域が広いと、異なる電位間の距離が大きくなり、電界が減少する。一方で、ソースとドレインの寄生抵抗が大きくなるという問題もある。
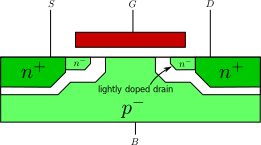
図7 LDD構造[1]
参考文献
[1] MOSFET short channel effects
http://www.onmyphd.com/?p=mosfet.short.channel.effects
[2] Wikipedia; ドレイン誘起障壁低下
https://ja.wikipedia.org/wiki/%E3%83%89%E3%83%AC%E3%82%A4%E3%83%B3%E8%AA%98%E8%B5%B7%E9%9A%9C%E5%A3%81%E4%BD%8E%E4%B8%8B
[3] Narain Arora (2007). Mosfet Modeling for VLSI Simulation: Theory And Practice. World Scientific. p. 197, Fig. 5.14. ISBN 981-256-862-X
[4] 伝情報通信学会 知識の森、S2群1編 デバイスの微細化限界とその物理
3章 微細デバイスの諸問題
https://ieice-hbkb-public.jpn.org/portal/doc_632.html
[5] 松田順一, 微細化による特性への影響
平成26年度 集積回路設計技術・次世代集積回路工学特論資料

最近のコメント