このページでは、面方位が異なる結晶格子面がなす角度を計算する方法についてまとめます。
X線回折測定をするときに非対称面を観察するためにω、2θを何度に設定すればいいのか、計算するためにまとめたものになります。
最後の結果を公式として覚えておけば、面指数を決めれば簡単に計算することが出来ます。
面のなす角を求めるには
一般的に、面のなす角は、面の法線ベクトルのなす角と等しいです。そのため、法線ベクトル同士の内積から求めることが出来ます。
二つの面の法線ベクトルを![]() とすると、
とすると、
![]()
ここで、![]() が、二つの面のなす角となります。
が、二つの面のなす角となります。
逆格子ベクトルを使う
格子面の法線ベクトルを求めればよいことがわかりました。では、どうやって法線ベクトルを求めるか、となります。
実は、結晶面の場合には、とあるベクトルが格子面に垂直であることが知られています。そのベクトルとは、逆格子ベクトルです。
(逆格子ベクトルが格子面に垂直であることの証明は、この後紹介するページのAppendixに記述しています。)
したがって、逆格子ベクトルの内積を計算すれば格子面のなす角を求めることが出来ます。![]() 面の逆格子ベクトルを
面の逆格子ベクトルを![]() とし、
とし、![]() 面と
面と![]() 面のなす角を
面のなす角を![]() とすると、
とすると、
![]()
となります。
また、![]() 面の格子面間隔を
面の格子面間隔を![]() とすると、
とすると、
![]()
という関係が成り立ちます。
立方晶の場合
立方晶の場合、逆格子ベクトル![]() は次のようにあらわされます。
は次のようにあらわされます。
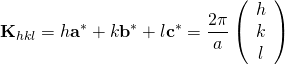
あとは式(1), (2)のように、内積を計算すると、
![]()
が得られます。
六方晶の場合
六方晶の場合、逆格子ベクトル![]() は次のようにあらわされます。
は次のようにあらわされます。
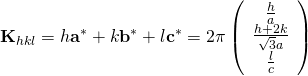
あとは式(1), (2)のように、内積を計算すると、
![]()
が得られます。
まとめ
格子面がなす角度を計算するために、格子面の法線ベクトル、特に逆格子ベクトルを使う方法を紹介しました。結晶格子として立方晶の場合と六方晶の場合の2通りの結果を示しました。最終結果だけでも覚えておけば、任意の格子面同士のなす角を簡単に求められます。これ以外の結晶格子でも同様に計算することができます。

2 comments on 結晶格子面のなす角を導出する