これまで、結晶格子の面間隔を計算したり、格子面がなす角度の計算を紹介してきました。
最後に、逆格子点が回折面上のどこに来るのかを、計算してみましょう。
回折ベクトルの定義
X線の入射、反射はXZ平面で起こるとすると、回折ベクトル![]() は、次のようにあらわされます。
は、次のようにあらわされます。
![]()
![]() の定義の仕方はいくつかあるのですが、ここでは、
の定義の仕方はいくつかあるのですが、ここでは、![]() とします。
とします。![]() はX線の波長です。
はX線の波長です。
回折面上での逆格子点の位置を計算する
それでは、![]() 座標で各面の回折点がどこにくるのか計算しましょう。
座標で各面の回折点がどこにくるのか計算しましょう。
まずはx軸とz軸を決めます。ここでは、x軸は[100]とし、z軸は[001]としましょう。
次に![]() を計算します。面指数(h k l)が決まれば面間隔を計算できます。
を計算します。面指数(h k l)が決まれば面間隔を計算できます。
ブラッグの法則から、![]() が計算できます。
が計算できます。
次に![]() を計算します。対称面、(00n)の場合は
を計算します。対称面、(00n)の場合は![]() で良いですが、
で良いですが、
非対称の場合は、異なります。
まず、(001)面と(h k l)面のなす角度![]() を計算します。
を計算します。
求めた角度を使って、![]() と計算できます。
と計算できます。
![]() の符号がプラスになるかマイナスになるかは、面指数lの符号によります。
の符号がプラスになるかマイナスになるかは、面指数lの符号によります。
ここまで来たら、逆格子点を計算することは簡単にできます。
最後に、測定できない領域と構造因子から回折が観察できない点を除いてあげれば、逆格子点を計算することが出来ます。
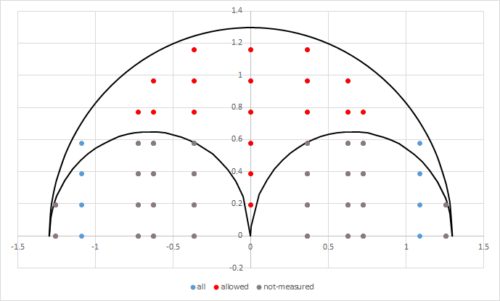
例えば、GaNについて計算した結果を図に示します。z軸は[001], x軸は[100]の結果と[110]の結果の両方を載せてあります。
青色は計算で求めたすべての逆格子点、グレーは観察できない領域、赤色は構造因子も考慮して、観察できる逆格子点です。
参考記事

最近のコメント