結晶格子の面間隔を計算する方法について、紹介します。今回は六方晶について説明します。
結晶格子の面間隔を計算する理由
結晶構造を調べる際の代表的な手法の一つにX線回折(XRD: X-Ray Diffraction)測定があります。XRD測定では結晶の格子面で反射したX線の強度と反射角を測定して、結晶構造を調べることができます。また、測定した結晶の結晶性がどのくらい良いか評価することもできます。
XRD測定をするときに反射したX線のピーク角度から格子面間隔を求めることができますが、その面が結晶のどの面なのかを判断する必要があります。そんなときに指定の格子面の面間隔を計算できることは役に立ちます。逆に、X線の反射がどの角度で起こるかを知ることが出来るので、測定範囲を適切に決めることができます。(測定に時間がかかってもいいなら別ですが・・・)
といっても、最近は測定・解析ソフトで簡単に計算できますが・・・
逆格子ベクトルを用いる
格子面の面間隔を計算するには逆格子ベクトルを用いるのが簡単です。
実格子ベクトルa, b, cに対応する逆格子ベクトルをa*, b*, c*とすると、
![]()
![]()
![]()
のように定義されます。
今、![]() 面の格子面間隔を求めることを考えます。
面の格子面間隔を求めることを考えます。![]() 面は、
面は、![]() のそれぞれ
のそれぞれ![]() に切る平面です。このとき、
に切る平面です。このとき、![]() 面の逆格子ベクトルを
面の逆格子ベクトルを![]() とすると、逆格子ベクトルは
とすると、逆格子ベクトルは![]() 面に垂直になります。
面に垂直になります。
そして、![]() 面の格子面間隔
面の格子面間隔![]() は、
は、
![]()
と表されます。
六方晶の場合の格子面間隔
では、立方晶の格子面間隔を求めます。図のように、実格子ベクトルを定義すると、実格子ベクトルは次のようにあらわされます。(![]() 軸方向のベクトルは、底面に垂直な方向です。)
軸方向のベクトルは、底面に垂直な方向です。)
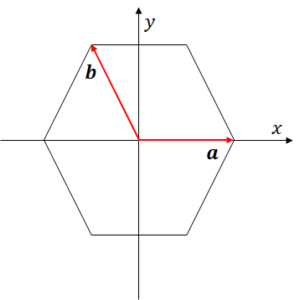
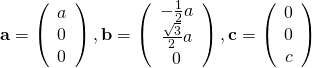
ここで、![]() は、六方晶の格子定数です。
は、六方晶の格子定数です。![]() の逆格子ベクトル
の逆格子ベクトル![]() は、
は、
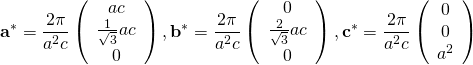
したがって、![]() 面の逆格子ベクトル
面の逆格子ベクトル![]() は、
は、
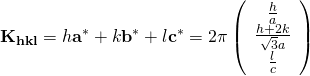
となります。このとき、
![]()
となるので、![]() 面の格子面間隔
面の格子面間隔![]() は、
は、
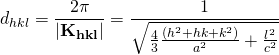
となります。
AlN, GaN, InNの格子面間隔
六方晶の結晶の例として、AlN, GaN, InNのいくつか代表的な面について計算した結果を示します。
| 格子定数 | AlN | GaN | InN |
| 3.11 | 3.19 | 3.54 | |
| 4.98 | 5.19 | 5.70 |
| 格子面 | |||
| (001) | |||
| (002) | |||
| (004) | |||
| (110) | |||
| (102) |
Appendix 逆格子ベクトルが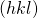 面に垂直であることの証明
面に垂直であることの証明
逆格子ベクトル![]() が
が![]() 面に垂直であることを示します。
面に垂直であることを示します。
![]() 面上の2つのベクトル
面上の2つのベクトル![]() と逆格子ベクトル
と逆格子ベクトル![]() の内積は、いずれも0になります。したがって、逆格子ベクトル
の内積は、いずれも0になります。したがって、逆格子ベクトル![]() は
は![]() 面に垂直になります。
面に垂直になります。
参考URL・参考文献
[1]井田隆, “格子面間隔値(d 値)の計算”
[2]慶應義塾大学理工学部物理情報工学科 伊藤研究室 講義資料

3 comments on 格子面間隔の計算方法-六方晶-