今回は、半導体中で起こる光に関係する現象のうち、光の放出過程と放出される光のスペクトルについて紹介します。LEDやレーザー、フォトダイオードの原理と関係がある内容となっています。
電子、正孔と格子の相互作用
半導体の中で起こる電子、正孔と光子の相互作用は大きく分けて3つあります。
(a) 価電子帯にある電子が空の電帯に励起されるときにおこる光子の吸収
(b) 伝導帯にある電子が価電子帯に自然に戻るときにおこる光子の放出
(c) 半導体に入射した光子が電子と正孔の再結合を結城佐瀬、同じエネルギーをもった光子を放出させる
(a)の過程は吸収と呼ばれ、(b)の過程は再結合あるいは自然放出呼ばれます。ちょうど自然放出は吸収の逆過程になっています。
(c)は誘導放出呼ばれ、光子によって誘起されて出てきた新たな光子は入射した光子とコヒーレントな状態になっています。
(a)はphotoディテクターや太陽電池で、(b)はLEDで、(c)レーザーで利用されています。
(レーザーは、LASER: Light Amplification of Stimulated Emission of Radiationの頭文字です。直訳すれば、誘導放出による光の増幅となります。)
ここでは、(b)自然放出の過程をもう少し見ていきましょう。
電子のバンド間遷移
自然放出、あるいは吸収、の過程では、バンドギャップの価電子帯から伝導帯に電子が遷移します。
この時、電子と正孔、光子は運動量保存則に従います。
英語では、この関係をk-selection ruleと呼びます。日本語訳すると、k-選択則といったところでしょうか。
この保存則を書き表すと、次のようになります。
![]()
ここで、![]() はそれぞれ伝導帯の電子の波数ベクトル、価電子帯の正孔の波数ベクトル、光子の波数ベクトルを表しています。
はそれぞれ伝導帯の電子の波数ベクトル、価電子帯の正孔の波数ベクトル、光子の波数ベクトルを表しています。
さて、電子、正孔の波数ベクトルの大きさと、光子の波数ベクトルの大きさを比較してみましょう。
電子と正孔の波数ベクトルの大きさは、
![]()
です。![]() は格子定数です。一方、可視光の光子の波数ベクトルは、
は格子定数です。一方、可視光の光子の波数ベクトルは、
![]()
です。両者を比べると、光子の波数ベクトルの大きさは電子と正孔の波数ベクトルの大きさよりも十分に小さいことがわかります。
したがって、光子の運動量は無視することが出来て、先ほどの保存則は、
![]()
と書き表されます。したがって、許容される遷移は電子と正孔の波数ベクトルが等しい遷移となります。このような遷移を直接遷移、もしくはE-kプロットで見ると垂直に電子が遷移することから、垂直遷移と呼ばれます。
では、伝導帯の下端と価電子帯の下端が異なる波数ベクトルをもつ場合、電子の遷移は起こらないのでしょうか?
このような場合、運動量を一定に保つためにフォノンによるアシストが必要になります。
すなわち、
![]()
という関係が成り立ちます。このような遷移を間接遷移と呼びます。
ただし、間接遷移の確率は低く、ほとんど起こりません。
間接遷移型の半導体でも光の放出を増やすための手段として、”特別な”ドーパントを添加する方法があります。
どう”特別”なのかは、別の記事で紹介します。。。
放出スペクトル
それでは、放出光のスペクトルについて計算してみましょう。
これまでバンド間の再結合では、ちょうど伝導帯の下端と価電子帯の上端に電子と正孔が存在すると仮定していましたが、実際には違います。温度が絶対零度でなければ、温度によるエネルギーの分だけ、電子は価電子帯の下端よりわずかに上側に、正孔は伝導帯の上端よりわずかに下側に位置しています。結果として、再結合によって放出される格子のエネルギーもバンドギャップよりわずかに大きいエネルギーとなります。放出された光子のエネルギーは次の関係で表されます。
![]()
この式は結合分散関係(joint dispersion relation)と呼ばれ、![]() は換算質量で、
は換算質量で、
![]()
と定義されます。換算質量をもつ粒子と考え、電子と正孔と同じように状態密度を計算すると、
![]()
となります。これを結合状態密度(joint density of states)と呼びます。
電子と正孔の分布は、伝導帯、あるいは価電子帯がフェルミ準位から十分離れていれば、すなわち非縮退であれば、ボルツマン分布
![]()
に従います。したがって、自然放出によって放出される光の強度は、
![]()
と表されます。
この式からわかるように、自然放出の閾値は![]() であり、ピークは、
であり、ピークは、![]() となります。
となります。
スペクトルの半値幅は、![]() で近似できることが知られています。また、この半値幅を波長になおすと、
で近似できることが知られています。また、この半値幅を波長になおすと、
![]()
となります。![]() は光速で、
は光速で、![]() の両辺を
の両辺を![]() で微分することで、上の式を導くことが出来ます。
で微分することで、上の式を導くことが出来ます。
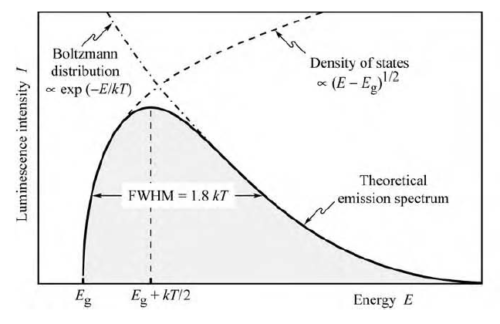
自然放出光のスペクトル[1]
参考文献
[1] E. F Schubert, “Light-Emitting Diodes” 2nd. , Cambridge University Press (2006).

最近のコメント