半導体において、エネルギーと運動量の関係、![]() 関係は様々な半導体の物性、物理を考えるうえで重要となります。例えば、フォトンやフォノンの相互作用というのは、エネルギーと運動量が一定に保たれていますし、電子と正孔の相互作用はエネルギーギャップを生じさせます。
関係は様々な半導体の物性、物理を考えるうえで重要となります。例えば、フォトンやフォノンの相互作用というのは、エネルギーと運動量が一定に保たれていますし、電子と正孔の相互作用はエネルギーギャップを生じさせます。
ここでは、半導体のエネルギーバンドとエネルギーギャップについて基本的なことをまとめ、GaN, AlNのエネルギーバンド図を示します。
エネルギーバンドの形成
結晶のバンド構造、すなわちエネルギーと運動量の関係は、多くの場合1電子近似のシュレーディンガー方程式を解くことで得られます。
このとき、結晶中のポテンシャル![]() は結晶格子で周期的なポテンシャルになっているというブロッホの定理が最も重要な定理になります。波動関数を
は結晶格子で周期的なポテンシャルになっているというブロッホの定理が最も重要な定理になります。波動関数を![]() とするとシュレーディンガー方程式は、
とするとシュレーディンガー方程式は、
![]()
となります。ブロッホの定理から波動関数はブロッホ波で書くことができ、
![]()
となります。![]() は実格子のサイズ
は実格子のサイズ![]() の周期をもつので、
の周期をもつので、
![]()
が成り立ちます。これが、![]() と等しくなるためには、
と等しくなるためには、![]() が
が![]() の整数倍である必要があります。したがって、
の整数倍である必要があります。したがって、![]() 関係を図にする際には逆格子ベクトル
関係を図にする際には逆格子ベクトル![]() を使うことができます[1]。
を使うことができます[1]。
ブロッホの定理からエネルギー![]() は逆格子ベクトル
は逆格子ベクトル![]() の周期をもちます。すなわち、
の周期をもちます。すなわち、![]() が成り立ちます。そのため、
が成り立ちます。そのため、![]() 関係を記述するには、逆格子の単位胞を考えれば十分となります。そこで、実空間のウィグナー・ザイツセルを逆格子空間にした第一ブリルアンゾーンが用いられます。
関係を記述するには、逆格子の単位胞を考えれば十分となります。そこで、実空間のウィグナー・ザイツセルを逆格子空間にした第一ブリルアンゾーンが用いられます。
このシュレーディンガー方程式を解くことでエネルギーバンド図が計算できます。ですが、解析的に解くことはできないため、数値計算によって解かれています。解くための手法としては平面波近似、擬ポテンシャル法、kp摂動法などがあります。
GaNとAlNについて計算された結果を下図に示します[2]
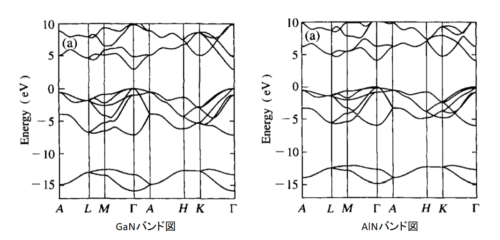
また、バンドギャップは温度依存性をもっており、半経験的に
![]()
で表されます。GaN, AlNの場合はそれぞれ、
![]()
![]()
となります[3, 4]。
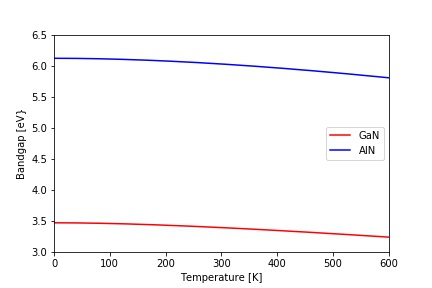
GaN,AlNのバンドギャップの温度依存性
有効質量
バンド単付近では、
![]()
が成り立ちます。ここで、![]() は有効質量と呼ばれます。この有効質量は一般的にテンソル表記で表され、
は有効質量と呼ばれます。この有効質量は一般的にテンソル表記で表され、
![]()
となります。ここで、キャリアの群速度は、
![]()
で表されます。
参考
[1]逆格子ベクトルについては、こちらの記事に書いています。
[2] 三輪和利, 福本敦勇、”ワイドバンドギャップ半導体GaN,AlNの物性予測 -第一原理計算による電子状態計算-”、豊田中央研究所 R&D レビュー Vol. 29 No. 4 ( 1994. 12 )
[3] GaNのバンドパラメータ:Bougrov V., Levinshtein M.E., Rumyantsev S.L., Zubrilov A., in Properties of Advanced SemiconductorMaterials GaN, AlN, InN, BN, SiC, SiGe . Eds. Levinshtein M.E., Rumyantsev S.L., Shur M.S., John Wiley & Sons, Inc., New York, 2001, 1-30.
[4] AlNのバンドパラメータ:Guo, Q, Yoshida A., Jpn. J. Appl. Phys. 33, part 1, 5A (1994), 2453-2456.

最近のコメント