状態密度関数を求めた際に、有効質量![]() と表され、これを状態密度有効質量と呼びます。この状態密度有効質量がどのように導出されるのでしょうか。
と表され、これを状態密度有効質量と呼びます。この状態密度有効質量がどのように導出されるのでしょうか。
まず、波数が![]() の間にある電子の状態数は、
の間にある電子の状態数は、
![]()
と表されます。
エネルギーが
![]()
のとき、
![]()
となります。もし、![]() が、
が、
![]()
の場合はどうすればよいでしょうか。ここで、次のような変数変換
![]()
を行うと、
![]()
となります。ここで、
![]()
![]()
より、
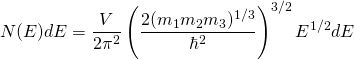
が得られ、したがって![]() と表されます。
と表されます。
正孔に関しては、重い正孔と軽い正孔の二つがあるので、状態密度は2つの和で表されるため、状態密度有効質量は、
![]()
となります。
以上が、状態密度有効質量の導出になります。
参考文献
[1] 御子柴 宜生 著、半導体の物理

最近のコメント