エピタキシャル成長した結晶の品質をはかる指標に転位密度があげられ、転位が少ないほど品質が良い。転位密度はX線回折測定によって、各面方位の半値幅を評価することで算出することができる。この記事ではGaNのエピタキシャル層の転位密度を求めることを考え、XRD測定で得られた半値幅から転位密度に換算する式を紹介する。
半値幅と転位密度の関係式
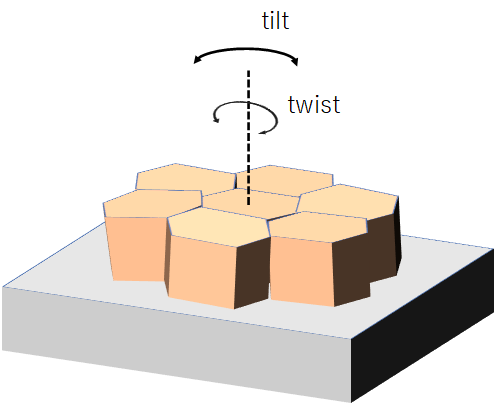
面のロッキングカーブの半値幅は結晶面の傾き(tilt)や回転(twist)によって広がる。
この半値幅の広がりと転位密度の関係は理論式で表され、半値幅から転位密度を算出することが可能である[1]。
転位が結晶にガウス分布に従って均一に存在している場合、
となる。
一方、粒界に転位が集中していると考える場合は、
で表される。
は転位のバーガースベクトル、
はバーガースベクトルと直交する面のロッキングカーブの半値幅、
は粒径である。
式の単位を考えるとわかるが、半値幅は単位なし、すなわちラジアンで表現される。
半値幅は通常、arcsecを単位として使うことが多いため、上記の式で転位密度を算出する際には気を付けたい[3]。
六方晶GaNの転位密度の評価
六方晶GaNの場合にはらせん転位のバーガースベクトルが
, 刃状転位のバーガースベクトルが
であることがTEMの解析から知られている。
<0001>は結晶の傾き、tiltを反映し、<11-20>は結晶の回転、twistを反映する。
さて、X線回折測定によって半値幅を求めることになるのだが、ここで問題になってくるのが、消滅則とX線回折装置の問題で測定できる面が限られることである。
消滅則からまずは考える。六方晶では、ミラー指数
が
または
を満たすときに観測可能である。
そのため、(0001)面は観測不可能であり、代わりに(0002)面を測定する。結晶の表面に(0001)面がくる場合、(0002)面を測定することは容易である。
一方、(11-20)面を測定する場合、完全に結晶内部の面を測定する、in-plane測定になるため、測定の難易度が上がる。
そこで、できるだけin-planeに近い面で測定し、そこから経験則で(11-20)面の半値幅を見積もる方法がとられる[4]。
(0002)から(10-15), (10-13), (10-11), (30-32)と徐々に(11-20)面に近づけていくと、(0002)面の半値幅はらせん転位が100%占めているが、徐々に刃状転位が占める割合が増えていく。経験則から、(30-32)面の半値幅の1.14±0.04倍した値を使うことで刃状転位の転位密度を算出することができる。
したがって、GaNのらせん転位密度と刃状転位密度は、転位が均一に存在していると仮定した場合、次のように算出される。
参考文献
[1] R. Chierchia, “Strain and crystalline defects in epitaxial GaN layers studied by high-resolution X-ray diffraction”
[2] 酒井, “選択横方向成長によって形成されたGaN膜 中の転位構造”, 電子顕微鏡 vol. 34, no. 3, pp. 197-199, (1999).
[4] H. Heinke, et. al., “X-ray diffraction analysis of the defect structure in epitaxial GaN”, Appl. Phys. Lett., vol. 77, pp. 2145 (2000).
最近のコメント